アナログとデジタルをつなぐ数学理工学部経営システム工学科　礒島伸教授 : 教員・研究紹介 : HOSEI ONLINE : 読売新聞オンライン

アナログとデジタルをつなぐ数学
理工学部経営システム工学科　礒島伸教授

礒島伸教授

アナログ量とデジタル量

世の中はさまざまな量であふれています。その中には、切れ目のない値を取るアナログ量（連続量）と、とびとびの値を取るデジタル量（離散量）とがあります。アナログ量には時間、距離、温度などが当てはまります。デジタル量は、１個、２個、......などと数えられる量で、人口などがあります。ただし、連続と離散は必ずしも対立するものではなく、同じ対象に両方の見方がある場合も多いことに注意してください。例えば、時間はアナログ量ですが、日常では時間・分・秒というとびとびの単位で捉えます。逆に、離散量を連続量であるかのように扱うこともあります。例えば、静止画像を十分に小さい時間幅で続けて表示することで、切れ目なく動いているように見えるのが動画です。

デジタルなモデルで交通流を再現

車社会の日本では、交通渋滞は大きな関心事です。その解消に向けて、数理の視点から何ができるでしょうか。渋滞が発生すると莫大な経済損失が生じるため、意図的に渋滞を起こしてデータを収集する実験を行うことはできません。そこで、交通の仕組みを表す数式を考えて、交通を理論的に再現する「おもちゃ（モデル）」を作り、そのモデルで実験して渋滞の対策を見いだします。その数式の作り方の一つとして、車1台1台が動くルールを数式で表現し、コンピューター上で動かす方法があります。このとき、すべてをデジタル量として考えると、理解しやすいモデルを作ることができます。ここでは一番やさしいものをご紹介します。

単純化するため、一方通行の1車線道路で考えます（図１）。本来、道路は連続している物体ですが、適当な長さの区画に分けて第1区画、第2区画、......とデジタル量で捉えます。また、各区画には車が1台入っているか、いないかのどちらかであるとします。さらに、交通状況を、1台の車が区画間を移動したかどうかが分かる程度のとびとびの時刻で観測します。そして車は、直前の区画が空いていれば次の時刻にそこへ進み、空いていなければ今の区画に留まるという規則で（ただし、移動できるかどうかをすべての車で判断してから一斉に）移動します。この簡単なモデルで、交通流の基本を捉えることができます。ただし、先頭の区画は一番後ろの区画につながっている（環状道路になっている）としています。より現実に近づけるには、前方区画に進む確率を導入する、停止している車が発車するまでのタイムラグを設定するなど、さまざまな設定を追加します。

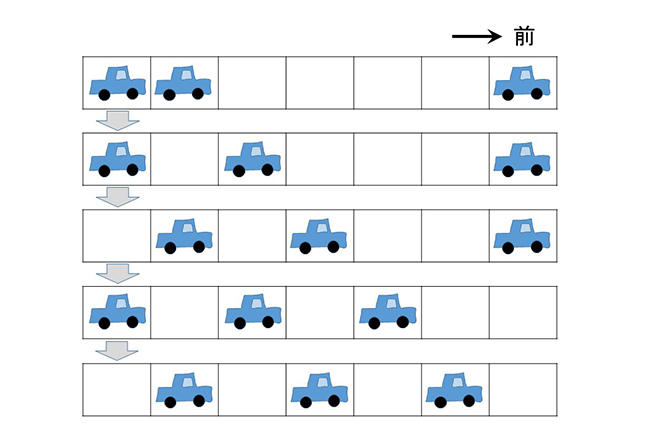
図1 交通流を理論的に再現するモデルの一例

壊れない波・ソリトン

無限個の箱を横一列に並べます。箱は、何番目であるかを数えられるので離散量です。箱には、1個の玉を入れることができるとします。いま、有限個の玉を用意していくつかの箱に1個ずつ入れ、これを時刻0の状態とします（図２）。これらの玉を、次のルールで動かします。「まず、一番左にある玉を、右側にある一番近い空箱に移す（①）。次に、まだ動かしていない玉の中で一番左にある玉を、右側にある一番近い空箱に移す（②）。この要領で、すべての玉を１回ずつ動かす」。すべての玉を動かしたとき、これを時刻1の状態とします。以下、前述のルールを繰り返していきます。このモデルを「箱玉系」といいます。

玉の動きを観察すると、次の特徴が分かります。N個の玉が連なっていて前方に十分な空箱がある場合、この玉の集団（波と呼びます）は1時刻につきN箱分進みます。つまり、長い波ほど速く進み、長さの異なる波がある場合は（より長い波が後ろにあれば）、波同士はいずれ衝突し、波の長さも崩れます。しかし十分に時間が経つと、必ず元の長さを持った波に分かれ、長さという「波の個性」は衝突によって破壊されはしません。

このような性質を持つ波の集団を「ソリトン」といいます。現実では、津波はソリトンの性質を持つ波とされています。歴史的には、偏微分方程式という連続量を扱う数式で最初に記述された現象で、理解するには大学の理系学部レベルの知識が必要です。しかし、箱、玉、整数の時刻というとびとびの量だけを用いることで、簡単に、かつ本質がより明確になり、高校生でも理解できる表現になっています。このような例をもっと増やし、さまざまな現象を理解する新しい数学を作っていきたいのです。

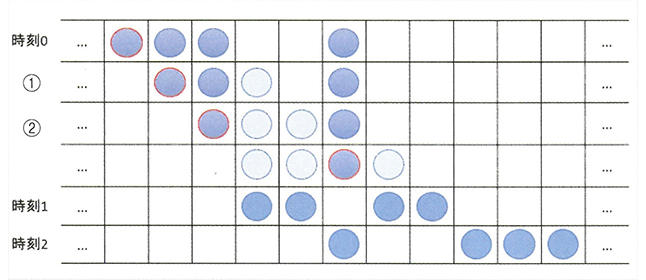
図2 箱玉系モデルの一例。上の4列が動かすルールで、赤枠が動かす玉、薄い色は動かした玉

連続の数学と離散の数学の交流を深める

本稿で述べた内容は、私自身が得た研究成果ではありません。連続量を扱う数学と離散量を扱う数学をつなぐ「超離散化」という技法の研究が、現在の私の専門です。本稿では交通流も波もデジタル量で説明をしましたが、実は両方ともアナログ量の数学モデルがあり、超離散化によって直接対応することが分かっています。しかし、この技法は制約も大きく、いつでもアナログ量とデジタル量を対応付けられるわけではありません。

膨大な計算が必要となる離散量の研究の歴史は、数学の中では浅く、いろいろな知見を蓄積する必要があります。離散量は近年のデジタル計算機と相性が良く、また、計算機の発展によってその研究が現実味を帯びてきたという見方もあります。超離散化の技法をさらに拡張し、研究の蓄積によって豊かな連続の数学と、新しい離散の数学との交流を深めていくのが私の目標です。

（初出：広報誌『法政』2021年6・7月号）

理工学部経営システム工学科　礒島伸: Isojima Shin
1977年生まれ。2000年、東京大学教養学部卒業。同年、東京大学大学院数理科学研究科へ進学し、2005年、同博士課程（数理科学専攻）修了、博士（数理科学）取得。青山学院大学理工学部助教などを経て、2012年に法政大学理工学部経営システム工学科に准教授として着任。2018年より現職。専門は数学の非線形可積分系。