1. Kepler and regular polyhedrons

I’ve always loved stargazing. As I write this in late June 2015, it’s rainy season here in Japan—but if the clouds ever part during the evening hours, you’re sure to catch twinkling Venus and nearby Jupiter burning brightly in the western sky. To the east, you should be able to see Saturn shining in line with Antares in the constellation Scorpio.

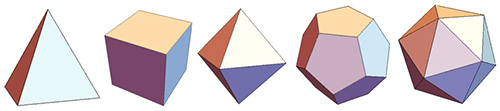
Johannes Kepler (1571–1630) is famous for his laws of planetary motion, but he also published some fascinating observations prior to discovering those laws. During Kepler’s time, only six planets had been discovered: Mercury, Venus, Earth, Mars, Jupiter, and Saturn. There were also only five regular polyhedrons known since Plato’s time: the regular tetrahedron (with four sides), regular hexahedron (or cube), regular octahedron (eight sides), regular dodecahedron (twelve sides), and regular icosahedron (twenty sides).

Kepler believed that there was some kind of relationship between the six planets orbiting the sun and the five regular polyhedrons. He started by considering a spherical surface (actually a thick spherical shell) that contains the orbit of Saturn. He inscribed a cube into that spherical shape, and then inscribed another spherical shell inside the cube, proposing that the inner shell would contain the orbit of Jupiter. He then continued in this pattern, placing a regular tetrahedron between Jupiter and Mars, a regular dodecahedron between Mars and the earth, a regular icosahedron between the earth and Venus, and a regular octahedron between Venus and Mercury（[1],[2]).

This model seems to be considered as nothing more than a personal flight of fancy, but the fact is that Kepler’s powerful desire to unravel the workings of the universe was what lead him to discover his three planetary laws. Even if you are not Kepler, you will feel mystified to find out that there are only five regular polyhedrons, while there are infinite regular polygons. Actually, mathematical objects called root systems have a lot to do with regular polygons and regular polyhedrons ([3]). Root systems come up in many different areas of modern mathematics and play an essential function.

2. Fullerene and variants of regular polyhedrons

If we relax the criteria for regular polyhedrons slightly, we will lose some symmetry—but we can also get several agreeable-looking shapes. For example, if we neatly cut a plane near each vertex of a regular polyhedron, we should get a regular polygon surface each time. The shape we are left with is called a truncated polyhedron. For example, a truncated tetrahedron would have four regular triangle faces and four regular hexagon faces. A truncated icosahedron would look like an angular soccer ball.

As you can see, the sides of these convex polyhedrons are made up of different regular polygons, but the area around each vertex is the same shape. We call this a semiregular polyhedron. It was Archimedes who first classified these shapes, and his work was later taken up by none other than Kepler ([2]).

Interestingly, the truncated icosahedron (soccer ball shape) is of deep importance in chemistry. Fullerene C₆₀, a carbon molecule made up of sixty carbon atoms arranged on the vertices of a truncated icosahedron, made headlines in the 1990s when the three chemists who verified its existence won the Nobel Prize. Literature [4] explains that the carbon atoms in Fullerene C₆₀ bind in 12,500 ways (resonance structures).

3. Polyhedrons and the problem of counting

Setting aside our discussion of shapes for a moment, I’d like to turn to another challenge:

You are given d positive integers: a₁ through a_d. Then say you have coins in front of you for the amount of each integer; for example, a₁-yen coins, a₂-yen coins, and so on all the way up to a_d-yen coins. You have as many of each coin as you need. If we say that n = 1, 2, 3, and so on, how many different ways are there to use your coins to pay for something that costs n yen?

Let’s say d = 2, a₁ = 1 and a₂ = 2. There is one way to pay 1 yen, two ways to pay 2 yen (two 1-yen coins or one 2-yen coin), two ways to pay 3 yen (three 1-yen coins or one 1-yen coin and one 2-yen coin), and so on. If we express this by using a mathematical formula, the question becomes as follows: How many sequences (m₁,…,m_d), of d nonnegative integers are there, which satisfy the equation:

a₁m₁ + a₂m₂ + … + a_dm_d = n?

In fact, solving this problem completely is exceptionally difficult. See reference [5] to find out what happens when d = 2, 3, and 4.

Now let’s consider what this means geometrically. The set of all the sequences (x₁,…,x_d) of d nonnegative real numbers, which satisfy the equation

a₁x₁ + a₂x₂ + … + a_dx_d = n,

becomes a polyhedron of (d – 1) dimension. For example, a point if d = 1, a line segment if d = 2, a triangle if d = 3, and a tetrahedron if d = 4. Now, let’s use this information rephrase the problem above as

“How many integer points (points whose coordinates are all integers) are there in this polyhedron?”

(The figure below shows a shape with seven integer points, where d = 3, a₁ = 1, a₂ = 2, a₃ = 3, and n = 6.)

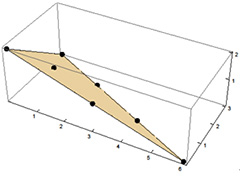
In this way, higher-dimension polyhedrons naturally appear in the problem of counting. If we use a more general scenario, we will start coming up with an endless number of complex polyhedrons. Mathematicians have been actively researching polygons from this perspective as well ([5]), which is playing a critical role in finding out more about the structure of certain kinds of spaces (aside from polyhedrons) of interest in modern geometry. And here again, root systems are involved in these lines of inquiry.

4. Professor Ichiro Satake

In section two above, I cited Prof. Ichiro Satake’s serial publication on Fullerene. People working in the sciences are probably most familiar with him as the author of Linear Algebra (Shokabo). He is also famous for his scholarly work with the root systems mentioned several times above. Prof. Satake was Professor Emeritus at the University of California, Berkeley as well as at Tohoku University. Between 1991 and 1997 academic years, he taught at the Faculty of Science of Engineering, Chuo University. Science and Engineering. He dropped by the department of mathematics every once in awhile even after he left the university, while authoring [4] and other works. In his spare time he would entertain us with fascinating stories. Prof. Satake passed away last October. The immensity of his legacy and the warmth of his exceptional character is something that still moves me today. May he rest in peace.

Tatsuru Takakura
Professor, Faculty of Science and Engineering, Chuo University
Areas of Specialization: Geometry, Topology

Professor Takakura was born in Toyama Prefecture in 1964. He graduated from the School of Science, the University of Tokyo in 1987, going on to complete a master’s course in the Graduate School of Science, the University of Tokyo in 1989 and a doctoral program at the Graduate School of Mathematical Sciences, the University of Tokyo in 1994. After receiving his Ph.D. in mathematical sciences from the University of Tokyo, he went on to work as an assistant professor at the Faculty of Science, Fukuoka University and then as a full-time instructor, assistant professor, and then associate professor on the Faculty of Science and Engineering, Chuo University before taking up his current post in 2014.
Takakura is currently studying symplectic manifolds with group action as well as the topology of their quotient spaces. He is also working on the geometry and combinatorics of the convex polyhedrons involved in those structures.