データを使って何をする？意思決定の新手法を目指して：研究：Chuo Online : 読売新聞オンライン

データを使って何をする？意思決定の新手法を目指して

福永　拓郎（ふくなが　たくろう）／中央大学理工学部教授
専門分野　数理情報学

データ・情報をどう利用する？

　「AI」や「データサイエンス」という言葉を見ない日はない。こんな状況下でわざわざ言うまでもないことかもしれないが、現代社会では多くのデータが生まれている。様々なシステムが電子化された上に、ほとんどの人は常にインターネットにつながる端末を携帯し、頼んでもいないのに自身の生活をインターネット上に記録する。その結果として、社会のあらゆる動きを記録したデータが着々と蓄積されている。データが蓄積されたとしても、利用しやすい形で保存されていなかったり、誰でも利用可能な形で公開されていなかったりするなど、もちろん課題はまだまだ多い。しかし、世の中のデータ化の流れが着実に進んでいることは事実だ。

　ただ、大量のデータがあったとしても、それのみでは何も役に立たない。データから有益な情報を取り出し利用することで、初めて価値が出る。このうち、データから情報を取り出す技術については、近年の進歩が著しい。機械学習を用いれば、大量のデータを人間よりも正確に分類することが可能になりつつあるし、データの中に潜む傾向を発見するための技術も研究が進んでいる。では、そのように取り出した情報を活用するための技術についてはどうだろうか？

　手に入れた情報を元に、システムの運用やデザイン、施策を決めることを、「意思決定」という。私の最近の問題意識は、情報の取得手法の発展スピードに、意思決定手法の進化が追いついていないのではないかということである。本稿では、この問題意識から私がここ数年取り組んでいる、適応的最適化という手法について、簡単に紹介したい。

意思決定の技術数理最適化

　適応的最適化の前に、数理最適化について触れたい。数理最適化は、様々な選択肢の中から最も良いものを求める計算問題を計算機を用いて解くための技術である。数理最適化を用いて意思決定を行う際には、満たさなければならない条件や最適化したい数量を表した数理最適化問題を記述する。その上で、この数理最適化問題の解を計算すると、今後実行すべき計画や施策を与えてくれる。

　数理最適化の研究には長い歴史があり、今日の情報技術を支える重要な基盤となっている。例えば、ある地点から別の地点に行くための経路を検索する経路検索は、数理最適化のキラーアプリケーションの一つである。今や当たり前の技術のように思えるが、数千・数万どころか数億以上の経路の中から最も良い経路を選ぶのは簡単なことではない。そこで活躍するのが数理最適化というわけである。

　数理最適化は意思決定のための重要なツールだが、多様な情報を活用しようと思うと物足りないと感じる場面もある。例えば、多くの機械学習アルゴリズムでは、確定的な予測を一つ返すのではなく、「この道を通るには80％の確率で20分かかるが、20％の確率で30分かかる」というように、予測結果の確率分布が出力される。実際、皆さんもよく使うであろうGoogle MapではAPI経由で2地点間の移動時間を問うと、悲観的・通常・楽観的の3通りの予測を返してくれる。このような情報を活用することは。従来の数理最適化の枠組みでは難しい。

適応的最適化不確実な状況下での最適化

　上で挙げた場合のように不確実な情報が与えられる状況下での意思決定のための一つのアプローチが、適応的最適化である。適応的最適化は通常の数理最適化の枠組みを広げる枠組みである。不確実であったり曖昧性を含むような情報から計画を立て、計画の一部を実行し、実行の過程で得られた情報から計画をアップデートすることで、通常の数理最適化手法よりも良い性能を達成することを目指している。

　適応的最適化の威力について実感してもらうために、一つ具体例を挙げて考えよう。図1のような道路ネットワークで、出発地から目的地へ行く最短経路はどれだろうか？このネットワークでは、出発地から目的地へ行くにはA地点を通る経路と、B地点を通る経路の2種類ある。ただし、B地点から目的地には並行して多くの道路が通っている。道路の脇に書かれている数字は、その道路を通ったときの所要時間である。ただし、B地点から目的地へ向かう道路の所要時間はすべて確率的に決定されるとし、確率0.99で所要時間2、確率0.01で所要時間0、道路それぞれの所要時間は独立であるとする。

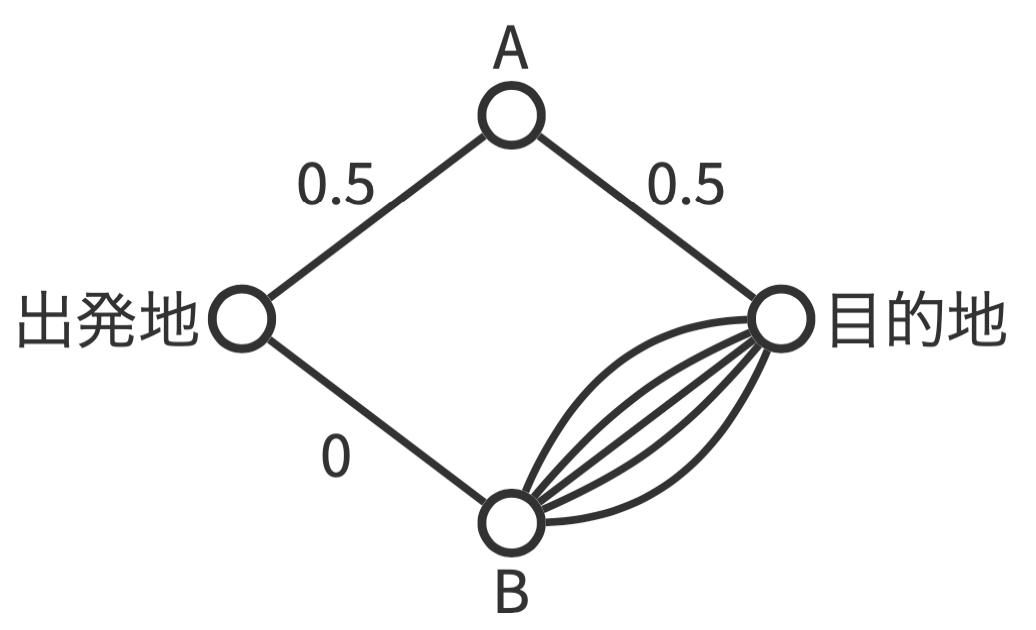
図1: 道路ネットワークの例

　このように確率的に定義されている最適化問題では、評価尺度の期待値が最良のものを最適解とするのが通常のアプローチである。上の例では、地点Aを通る経路の所要時間は常に1、地点Bを通る経路は並行した道路のどれを通ることにしても所要時間の期待値が1.98となり、地点Aを通る経路の方が所要時間の期待値が少なくなることが分かる。

　しかし、もっと良い方法があることに気付くだろうか？それは、目的地から地点Bまで行った上で、地点Bから目的地までの道路それぞれの所要時間を観測した上で、最も早く行ける道路を選んで目的地に向かうことである。地点Bと目的地を結ぶ1本の道路が所要時間0になる確率はごくわずかだが、並行して通る道路の数が多ければ、高い確率で少なくともどれか1本は所要時間0となる。よって、このような戦略を許せば、出発地から目的地へ向かう所要時間の期待値はほとんど0になる（正確な期待値の値は、地点Bと目的地間の道路の本数に依存する）。

　もちろん、このような戦略は反則だと思う人もいるかもしれない。これは結局、使う際にそのような観測をすることが許されているかどうか次第だ。適応的最適化は、確率的な事象をアルゴリズムの実行段階で観測できるという状況下で、そのような特長を生かしてより効率的な最適化を実現することを目指している。

最後に

　このように従来の数理最適化よりもポテンシャルを秘めた適応的最適化だが、もちろん課題も沢山ある。簡単に想像できるように、適応的最適化が扱う問題は従来の数理最適化で扱う問題よりも構造が複雑で難しい。効率的に解くことができるのかどうか、まだ分かっていない場合も多い。この技術が活用可能になるよう理解を深めていくことが私の目下の研究テーマである。

福永　拓郎（ふくなが　たくろう）／中央大学理工学部教授 専門分野　数理情報学: 名古屋市出身。1981年生まれ。2003年京都大学工学部卒業。2005年京都大学大学院情報学研究科修士課程修了。2007年京都大学大学院情報学研究科博士後期課程修了。博士（情報学）。
京都大学大学院情報学研究科助教、国立情報学研究所特任准教授、理化学研究所革新知能統合研究センター研究員、中央大学理工学部准教授を経て2021年より現職。

情報工学、特に離散アルゴリズムの理論と意思決定への応用に関する研究に従事。