ボトルネック型交通渋滞の実験研究：研究：Chuo Online : 読売新聞オンライン

ボトルネック型交通渋滞の実験研究

大坪　弘教（おおつぼ　ひろのり）／中央大学国際経営学部准教授
専門分野　実験経済学

1. 戦略的状況としてのボトルネック型交通渋滞

　都市における道路交通渋滞は、現代社会が抱える大きな問題の一つである。国土交通省道路局が 2015 年に発表した資料によれば、一人あたりの年間渋滞損失時間は乗車時間（約 100 時間）の 4 割に相当する約 40 時間であるという。このような膨大な量の時間の浪費に加えて、道路交通渋滞は騒音や大気汚染、CO₂排出といった環境への悪影響も生み出している。国や自治体は多くの資源を投入し、既存の道路の拡張や新たな道路の建設によって渋滞の解決に長年取り組んできた。しかし、一時的に渋滞を和らげることに成功しても、時間の経過と共に再び渋滞が発生する「いたちごっこ」のような状況が続いている。

　渋滞の原因は様々であるが、ボトルネックのある道路において発生する交通渋滞が知られている。ボトルネックとはその名の通り瓶（ボトル）の口のように狭くなっている箇所のことで、スムーズな車両の流れを妨げる。例としては橋、トンネル、料金所、道路工事現場などがあげられる。ボトルネックには一定時間に通過できる車両数の上限があるため、通過しようとする道路利用者が同じ時刻に集中してしまうと渋滞が発生してしまう。つまり渋滞の程度は、「いつ通過するか」という自分と他の道路利用者の意思決定によって決まるのである。

　自分が得られる利益や結果が、自らの行動のみならず他人の行動にも依存している状況のことを戦略的状況と呼ぶ。交通渋滞に限らず私たちの身の回りには戦略的状況で溢れている。勝ち負けを争うゲームやスポーツはもちろん、価格競争、紛争、資源獲得競争、オークション、交渉など枚挙にいとまがない。戦略的状況においては、各人は他の人々がどのように行動するかを勘案した上で自らにとって最適な行動を選択することになる。そのような状況における意思決定を分析する道具がゲーム理論である。

　ボトルネック型交通渋滞にゲーム理論を応用する研究は少しずつ増えている。しかし理論分析のみでは、理論予測が実際の人間の行動と乖離するのかどうか、また乖離しているとしたらどのように乖離しているのか、なぜ乖離するのかといった問いに答えることができない。実際に意思決定を行うのは生身の人間である。実験を通して人間の行動の特徴や傾向を把握することは既存研究の不足点を補い、結果として渋滞の発生や変移のメカニズムの解明に寄与すると考えられる。

2. 出発時刻決定問題

　ボトルネック型渋滞を分析するモデルとしては、Vickrey (1969)によって考案されたのちに、Arnott et al. (1990, 1993) らによって基本モデルが構築された単一ボトルネックモデルが有名である。図 1 はモデルが想定している交通ネットワークの形状を表したものである。居住地（O）から勤務地（D）に通じる 1 本の道路があり、その道路上にボトルネックが 1 つ存在している。全ての道路利用者は共通の希望到着時間に勤務地に到着することを望み、居住地からこの道路を通って勤務地に通勤する。ボトルネックを通過できる 1 単位時間あたり車両数には上限があり、全員が同時に通過することはできない（つまり、全員が希望到着時間に勤務地に到着することは不可能）。通勤にかかる移動費用は

(待ち時間およびボトルネック通過時間による移動時間費用)
+
(実際の到着時間と希望到着時間の差による早着費用または遅着費用)

で表される。各道路利用者は他の利用者の出発時刻を予想しながら、自らの移動費用を最小にするように出発時刻を選択する。

図 1: 単一ボトルネックを持つ道路

　ここでは、道路利用者（以下プレイヤーと呼ぶ）が 3 人（A さん、B さん、C さん）の場合の数値例を紹介する。この例では、以下の仮定を置いている。

各プレイヤーは移動費用（移動時間費用と早着費用または遅着費用との合計）を最小にするように居住地から勤務地へ向けて出発する時刻を選ぶ。
各プレイヤーが選択できる出発時刻は t = 0,1,2,3 の 4 つであり、勤務地への希望到着時刻は全員共通の t = 2 とする。
居住地からボトルネックの入り口までの移動時間、ボトルネック出口から勤務地までの移動時間はそれぞれ 0 とする。つまり、居住地を出発したと同時にボトルネックに到着し、ボトルネックを出発すると同時に勤務地に到着する。
ボトルネックを通過できるのは 1 単位時間あたり一人である。ボトルネックに到着するプレイヤーが 2 人以上の場合は、ランダムに順番が決まる。
移動時間は (勤務地到着時刻−居住地出発時刻) で計算し、移動時間費用は 1 単位時間あたり2 とする。
早着時間は(希望到着時刻−勤務地到着時刻)で計算し、早着費用は1単位時間あたり1とする。
遅着時間は(勤務地到着時刻−希望到着時刻)で計算し、遅着費用は1単位時間あたり5とする。

　表 1 は、A さんは t = 0 に、B さんと C さんは t = 1 に居住地を出発した場合の結果を表している。A さんはボトルネックでの待ち時間がなく通過したが、希望到着時間よりも 1 単位時間早着となった。B さんと C さんは同時に出発したため、どちらが先にボトルネックを通過するかはランダムに決められた。B さんが先に通過し、希望通りの時刻に勤務地に到着できた。C さんはボトルネック入り口で待たされ、希望到着時間から 1 単位時間遅着となった。

プレイヤー	出発時刻	ボトルネック		到着時刻	早着時間	遅着時間	移動費用
プレイヤー	出発時刻	待ち時間	通過時間	到着時刻	早着時間	遅着時間	移動費用
A	0	0	1	1	1	0	3
B	1	0	1	2	0	0	2
C	1	1	1	3	0	1	9

表 1: 数値例

　ゲーム理論を用いた分析の場合、ナッシュ均衡という状態に注目する。ナッシュ均衡とは、各プレイヤーの戦略（ここでは出発時刻）が他のプレイヤーの戦略に対して最適反応になっている状態のことである。言い換えると、他のプレイヤーが戦略を変えないとしたときに、自らが戦略を変えても得をしない安定的な状態である。戦略を変えることで得をするようであれば、その状態はナッシュ均衡ではない。

　表 1 の出発時刻の組み合わせはナッシュ均衡ではない。C さんは結果的に B さんの後にボトルネックを通過することになったが、ボトルネックの通過順はランダムに決まることから、t = 1 を選ぶときの C さんの（期待）移動費用は 2+9 2 = 5.5である。ここで C さんのみが出発時刻を t = 0 に変えたとしよう。A さんの出発時刻と重なるため、ボトルネックの通過順はランダムに決まる。待ち時間なく先に通過できた場合には希望到着時刻より 1 単位時間早着となるため、移動費用は 3 となる（移動時間費用 2 ＋早着費用 1）。A さんの後にボトルネックを通過する場合には、1 単位時間の待ち時間こそあるものの、希望到着時刻に勤務地につくことができる。このときの移動費用は 4 となる（移動時間費用 4 のみ）。よって、t = 0 を選ぶときの C さんの（期待）移動費用は 3+4 2 = 3.5 となる。つまり、出発時刻が t = 1 のときよりも（期待）移動費用を減らすことができる。他の二人が出発時刻を変えないとしたときに、C さんは出発時刻を t = 1 から t = 0 に変えるインセンティブがあるため、表 1 の出発時刻の組み合わせはナッシュ均衡ではない。

　ちなみに、この例のナッシュ均衡は 3 人とも t = 0 を選ぶというものであり、その時の 3 人の移動費用の合計は 18 である。表 1 の出発時刻の組み合わせでは 3 人の移動費用の合計は 14 であり、ナッシュ均衡での移動費用の合計を下回っている。3 人の移動費用の合計が最小になっている状態を社会的最適とすれば、ナッシュ均衡の出発時刻の組み合わせは社会的最適を達成できていないことが分かる。もし、t = 0 から t = 2 までの各時刻に一人が出発すれば、3 人の移動費用の合計は最小の 12 となり社会的に最適な状態になる。しかしこの状態ではプレイヤーごとに移動費用が異なること、また各プレイヤーの出発時刻は他のプレイヤーとの協調なしに自由に決定されることから、社会的最適な状態が分権的に達成されるとは考えにくい。

3. 実際の人間はどの出発時刻を選ぶのか

　今年度中に中央大学多摩キャンパスにて実施予定の実験では、実験 1 セッションあたり 10 人から 20 人ほどの学生をリクルートする予定である。プレイヤーの数や戦略の数が大きくなると、ナッシュ均衡の数も膨大なものになり、その導出もコンピューターを使った数値計算に頼らざるをえない。実験では全ての実験参加者に同じ費用構造が与えられるため、全てのプレイヤーが同じ戦略を用いる対称ナッシュ均衡を理論予測のベンチマークとして用いる。例えば、プレイヤーの数を 15 人、選択できる出発時刻を t = 0,1,2,...,20 の 21 個、希望到着時刻を t = 15、1 単位時間あたりの移動時間費用、早着費用、遅着費用を表 1 の例と同じと仮定した場合、各プレイヤーは図 2 の混合戦略を用いる（上：確率分布、下：累積分布）。これは各プレイヤーがこの図の確率分布に従って出発時刻を選ぶことを意味する。例えば、t = 8 の選択確率は 0.1581、t = 19 の選択確率は 0.0090 という具合である。

　では、生身の人間がこのゲームを複数回プレイした場合には、一体どの出発時刻を選択するのだろうか。各プレイヤーの行動はナッシュ均衡における戦略と一致するのだろうか。これまでの膨大な実験研究から次の結果が予想される。^[1](1) 集団レベルの選択頻度がナッシュ均衡で予想される選択確率に近似するが、(2) 個人レベルでは一括にすることが困難なほど多種多様で非合理な行動が見られ、均衡における選択確率に矛盾しない行動をとるのは一部の実験参加者に過ぎない。つまり、実験参加者一人一人は分類することが不可能なほどバラバラの動きをしていても、集団全体としてはナッシュ均衡に近い動きを見せることが予想される。

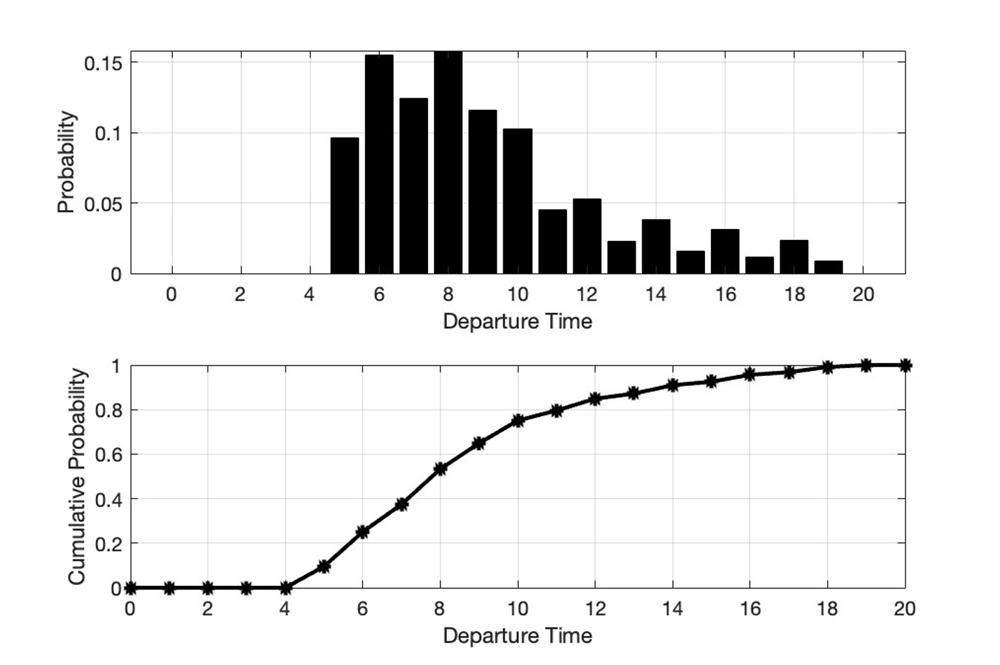
図 2: 対称混合戦略ナッシュ均衡

4. 今後に向けて

　個人レベルでナッシュ均衡からの逸脱の原因はいくつか考えられる。例えば、ゲーム理論では完全合理的なプレイヤーを想定しているが、実際の人間は極めて限定合理的なのかもしれない。さらに、普通に考えれば決して驚くべきことではないが、そもそも人々は同質ではなく異質である。プレイヤーの個性のばらつきをうまく捉えた均衡概念が必要なのかもしれない。候補としては、限定合理性を捉えることができる質的応答均衡（Quantal Response Equilibrium）に、プレイヤーの異質性を組み込んだモデルが考えられる。実験後のデータ分析を見据え、今後はこれら 2 つを加味したゲーム理論モデルの検討をすすめてまいりたい。

※本研究はJSPS科研費JP20K01554の助成を受けたものである。

[1] 混合戦略ナッシュ均衡に関する実験のサーベイは Camerer (2003) の第 3 章が詳しい。

[参考文献]

Arnott, Richard, André de Palma, and Robin Lindsey. 1990. Economics of a bottleneck. Journalof Urban Economics 27: 111-130.
Arnott, Richard, André de Palma, and Robin Lindsey. 1993. A structural model of peak-period congestion: A traffic bottleneck with elastic demand. American Economic Review 83: 161-179.
Camerer, Colin. 2003. Behavioral Game Theory. Princeton University Press, New Jersey.
Vickrey, William S. 1969. Congestion theory and transport investment. American Economic Review 59: 251-260.

大坪　弘教（おおつぼ　ひろのり）／中央大学国際経営学部准教授 専門分野　実験経済学: 福岡県大牟田市出身。1976 年生まれ。
2002 年5 月アメリカ・州立アリゾナ大学卒業。
2008 年8 月アメリカ・州立アリゾナ大学大学院博士課程修了。Ph.D.（経済学）。
ドイツ・マックスプランク経済学研究所ポストドクトラルリサーチアソシエイト、創価大学経済
学部講師、准教授を経て、2021 年4 月より現職。