ここでは私たちの研究室の鳥谷部さん、宗行、と東京大学大学院 理学系研究科の沙川さん、上田先生、佐野先生の共同研究となった、Toyabe, Sagawa, Ueda, Muneyuki, and Sano, “Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality", Nature Phys. 6, 988-992（2010）の前半の内容について、背景となる熱力学の第２法則やマックスウェルの悪魔から始めて、比較的平易な説明を試みようと思います。

１．熱力学第２法則

　熱力学第２法則は物理学の法則としては非常に珍しく、式を使わずに述べられる法則で、

クラウジウスの原理

それ以外に何の変化も残さずに低温物体から高温物体に熱を移すことは不可能である。

トムソンの原理

それ以外に何の変化も残さずに１つの熱源から吸収した熱をすべて仕事に変えることは不可能である。

という二つの言い方が良くされます。クラウジウスの原理はこれを破れれば温度差のないところから温度差を作ることができ、それを使って物体を膨張させたりして仕事をすることによりトムソンの原理を破れますし、トムソンの原理が破れれば、そこで得られた仕事で摩擦熱を発生して物体の温度を上げ、クラウジウスの原理を破れるので、結局両者は同じことを言っていることになります。この熱力学第２法則は決して破れることのないもっとも根本的な自然法則の一つです。

２．マックスウェルの悪魔

　以上のように熱力学第２法則は決して破れない法則ですが、なんとかしてそれを破ろうと、古くから多くの人がアイディアを出してきました。その中でもっとも有名なものの一つがジェームズ・マックスウェル（１８３１－１８７９）によるマックスウェルの悪魔で、クラウジウスの原理を破って温度差を作ろうとするものです。ここで温度が高いと言うことは、物質を構成する粒子が不規則に激しく動いている状態を指し、温度が低いと言うことは粒子の動きが鈍いことを指します。

　実際にすべての物質は温度に応じて揺らいでいて、その揺らぎは熱揺らぎと呼ばれます。例えば水中の水分子は１秒間に10¹³回も衝突しながら平均して秒速数百ｍで動いています。この水分子の衝突に突き動かされてマイクロメートル程度の大きさの粒子は水中でブラウン運動と呼ばれる不規則な動きを絶えず示します。このブラウン運動も熱揺らぎの一つです。

　したがって気体の入った容器の右を熱く、左を冷たくして温度差を作るには、平均の速さより速く動く気体の分子を右に、遅く動く分子を左に集めればよいのです。

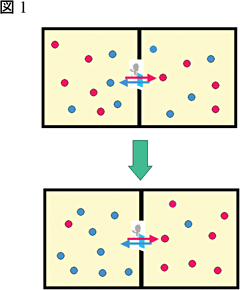
　そこでマックスウェルは容器の左右を仕切る扉を開閉する一匹の悪魔を考えました（図１）。この悪魔は右の部屋から遅い気体分子がくると扉を素早く開閉して左の部屋に通し、左の部屋から速い気体分子がくるとまた扉を素早く開閉し右の部屋に通すとしました。これを繰り返せば容器の右には速い気体分子、左には遅い気体分子が集まるでしょう。つまり左右に温度差が出来ることになります。

　気体分子は何にも触れずに扉を通過するのでエネルギーはもらいません。つまり、マックスウェルの悪魔がいると容器の中の気体分子はエネルギーをもらわないで、しかも容器の左右に温度差が出来るのです。これは前述のクラウジウスの原理を破るように見えます。そのため、このマックスウェルの悪魔は１８６７年の提案以来大論争を引き起こしてきました。しかしどこかにトリックがあるはずです。

　そこでもう一度マックスウェルの悪魔がしていることを整理すると、

1. 気体粒子の速度を観測する。
2. 観測して得た情報を記憶する。
3. 扉を操作して気体分子を通過させる。
4. 先に得た記憶を消去して次の粒子の到来に備える。

このうち扉の操作では粒子のエネルギーが変化しないことは先に説明しました。すると熱力学第２法則に反さずに悪魔が働くには１、２、４のステップのどこかでエネルギーを使うはずです。しかしこれらのステップは本質的に情報が絡む話で、当時物理学の中に情報というものはありませんでした。

　この問題にひとまずの解決が与えられたのは１９６１年に発見されたランダウアーの原理によってです。ランダウアーは４．の情報の消去のステップにエネルギーがいることを示しました。さらに２００９年に今回の研究の主役の一人である沙川さんが上田先生とともに取得と消去をあわせた情報のやりとりに必要なエネルギーには一定の制限があることを示し、これによってマックスウェルの悪魔は実はこっそりエネルギーを使っていたことが発覚したのです。したがって「マックスウェルの悪魔の実現」は、現在の理解では「エネルギーを使って情報を得、気体分子に直接働きかけることなくその動きを制御すること」になります。

３．マックスウェルの悪魔の実現

　ここまでの説明でマックスウェルの悪魔の実現は決して熱力学に反する話ではないことがおわかり頂けたかと思います。しかし実際にこれを作るのはそう簡単ではありません。

　まずマックスウェルの悪魔は、気体分子に直接手を下さずに移動させるのですが、それは気体分子が勝手にさまざまな速度で飛び回っているから出来たのでした。そして粒子が来たら扉を素早く開閉しなければなりません。

　ところで、何もしなくても熱によりさまざまな速度で物体が揺らぐということは、大きさがマイクロメートル程度の物体では実は普通のことです。実際に現在のナノテクノロジーの世界では非常に微小な物体を扱うので、温度を下げたり、大きなエネルギーを使って熱揺らぎを押さえようとしていますが、この世界はまさにマックスウェルの悪魔が活躍できる場でもあるのです。そしてこのような場でマックスウェルの悪魔を実現することは物理学として面白いだけではなく、微小スケールの世界での高速精密制御という技術面での挑戦的目標としても位置づけられます。これが出来れば熱揺らぎを押さえる代わりにそれを利用するという、今までとは逆の発想で物体の移動を制御する画期的な方法になります。この実験面での挑戦を引き受けたのが、この研究の主役の鳥谷部さんでした。

　ここでマックスウェルが考えたものをそのまま作ることはできないので、何かそれと同等なことをして粒子をエネルギーの低い位置から高い位置にうごかす、物理学の言葉で表すと粒子にポテンシャルエネルギーを与える、ことを目標にしました。

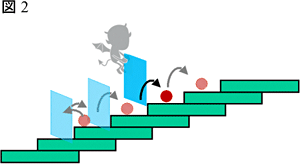
　まずマックスウェルの悪魔が使った情報は気体分子の速度でしたが、私たちは粒子の位置を使うことにしました。そして悪魔は扉にやってくる気体分子を交通整理したのですが、私たちの場合はたまたまポテンシャルの高いところに上った粒子（階段の上に上がった粒子、と思って頂いて結構です）の後ろに後戻りできない仕切を入れていくことにしました（図２）。ミクロの世界では激しい熱揺らぎで粒子はたまにポテンシャルの高いところに上るのです。マックスウェルの悪魔は一ヶ所にいて多数の粒子を仕分けして温度の高低を作ったのですが、私たちは一つの粒子を追いかけながらその後ろに仕切を入れて、高いところに追いやろうというわけです。仕切は粒子の後ろに入れるだけですから、直接粒子に働きかけることなく、結局マックスウェルの悪魔と同じように、粒子に関する情報を得てその粒子のポテンシャルエネルギーを上げるのです。

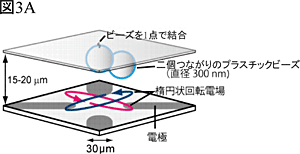
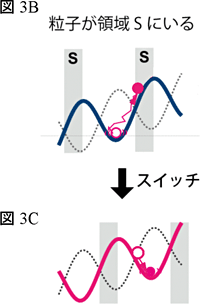
　ここで研究室にあったＦ１－ＡＴＰａｓｅという回転分子モーターの研究のための回転電場装置が役立ちました。この装置はガラス板の表面に４つの微細な電極が蒸着してあり、この電極に変化する電圧を加えてさまざまな電場を作れます。Ｆ１－ＡＴＰａｓｅの研究では回転する電場を作り、Ｆ１－ＡＴＰａｓｅに結合した直径０．３マイクロメートルほどの二個つながりのプラスチックビーズにポテンシャルをかけます。この装置で、私たちはＦ１－ＡＴＰａｓｅは使わずにプラスチックビーズを直接ガラスの表面に一点で結合させ（図３Ａ）、うまく電極にかける電圧を制御し、図３Ｂの様な電場によるポテンシャルの螺旋階段を作りました。このようなポテンシャルの上でプラスチックビーズは、回転ブラウン運動をして、たまには図の右方向の山に上りかけたり、時には山を越えたりもしますが、全体として左の低い側に動いて行きます。そこでプラスチックビーズを顕微鏡で観察してその位置がポテンシャルの右の上り坂の途中（図３ＢのＳと書かれた領域）に偶然来たときに電圧を切り替えて図３Ｂの点線のようなポテンシャル（＝図３Ｃの赤線）に替えました。簡単そうですが、正確なポテンシャルの作成、高速カメラで捉えたビーズの位置の瞬間的な処理とポテンシャルの切り替え、など非常に難しい問題をいくつもクリアしています。このようにしてポテンシャルが切り替わると（図３Ｃ）、ビーズは新しいポテンシャルによる右下がりの勾配の上にありますから左には行きにくくなります。これが仕切を入れたことに相当します。そして右側の下り勾配に従って右の谷に落ちて行くことが期待されます。この谷底はもとのポテンシャルの谷底より高いのでビーズは少し高いところに上ったことになります。これを繰り返すと、ビーズは徐々に図の右方向にポテンシャルの坂を上って行きます。ここでビーズが坂を上るときのエネルギーは熱揺らぎから供給されていていることに注意して下さい。つまり、これでビーズの位置を測定して領域Ｓにいたという情報をもとにポテンシャルを切り替え、ビーズに対しては直接エネルギーを与えずにポテンシャルの高い方向に移動させたことになります。これが本実験でのマックスウェルの悪魔なのです。

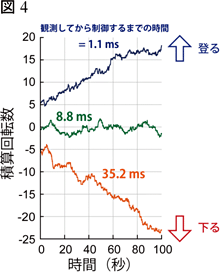
　ところで、マックスウェルの悪魔を実現するには素早い操作が必要だと述べました。実際、位置を観測したときにビーズが領域Ｓにいても、もたもたしているとポテンシャルを替えたときにはＳの外にいるかも知れません。そこでビーズの位置を測定してからポテンシャルを替えるまでの時間を変えてビーズの移動する様子を観察したのが図４です。たしかに１．１ミリ秒で素早く切り替えた時はビーズは坂を上れますが、８．８ミリ秒では上下がほぼ釣り合って、３５．２ミリ秒ではせっかくポテンシャルを替えてもビーズは坂を下ってしまいます。

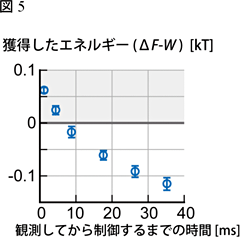
　ポテンシャルを替えたときにビーズが領域Ｓの外に出ている時にはビーズはポテンシャルを作る電場からエネルギーを受け取ることがあります。逆にビーズが領域Ｓにいる時にポテンシャルを替えるとビーズは電場にエネルギーを与えます。そこでビーズと電場のエネルギーのやりとりを厳密に計算し、ビーズが坂を登ることによって得たエネルギーとの差をグラフにしたのが図５です。素早くポテンシャルを替えたときはビーズの得たエネルギーが電場から得たエネルギーを上回ります。このようにして外から加えたエネルギー以上のエネルギーを情報によって物体に与えたことを正確に示したのは私たちの実験が初めてです。このエネルギー差は熱揺らぎからきていて一見、最初に述べたトムソンの原理を破るように見えますが、それはビーズの位置の情報をエネルギーを使って得たからできたのです。位置の測定に要したエネルギーも含めて考えれば熱力学第２法則は破れていません。

　原論文ではこの後、測定で得た情報量とビーズが得たエネルギーの関係や、一般化Ｊａｒｚｙｎｓｋｉ等式の検証など、重要な内容が述べられていますが、残念ながらこれらについて説明するには、スペースがありません。これらの理解のためには今一度基本からしっかり勉強するべきことが多々ありますので、もっと先まで知りたいと思った人は勉強してみて下さい。目を見張るような世界がこの先にありますから。