学校で使える数学遊びとして、「数学を用いた席替え」を提示する。席替えというと、くじ引きなどが一般的であるが、本稿では、くじを用いずに、誰にでもできる簡単な計算によって席替えを行う方法を紹介する。この方法は、生徒が「何でこうなるの？」と思えるいくつかの要素を含んでおり、数学について考えるきっかけになりうるものである。

くじ引きを用いない席替え

　いま、３２人のクラスにおける席替えを考える。黒板には１～３２の数字が書かれており、生徒は一人ずつ順番にそこから数字を一つ選び、選ばれた数字は消していく。こうすることで、各生徒は１～３２の中から互いに異なる数字を一つだけ選ぶことになる。最後に、教師の指示により、生徒は自分が選んだ数字を５２倍して３３で割った余りを求める。この求めた余りの値を新しい席とすることで、席替えは完了する。

（※席番号は廊下側の前から順に１，２，３…など、あらかじめ決めておく）

　例えば、５を選んだ生徒は、５×５２＝２６０，２６０÷３３＝７…２９　なので、２９番の席がこの生徒の新しい席になる。

　上記の方法について、３２人のクラスであれば割る数は３３で固定となる。これは割ったときの余りを１から３２のいずれかにするためである。一般に「クラスの人数＋１」で割る。一方、かける数は５２としたが、ここは別の数でもよく、初めに数字を選ぶ生徒にとっての不確定要素となる。

　ただし、かける数はどんな数でも良いというわけではない。注意すべきは、「余りが被らないようにする」ということである。当然ながら、生徒が求める余りは他の誰かと重複してしまうと席替えは成立しない。席替えを成立させるためには、余りをバラバラにする必要がある。

　結論から言うと、割る数３３，かける数Ａに対しては、Ａと３３が互いに素（Ａと３３の最大公約数が１）になるようにＡを選べばよい。

　何故これでうまくいくかという説明はいろいろと考えられるが、ここでは、生徒がなるべく楽しめるように「星の一筆書き」と絡めて、説明をしていく。

星の一筆書き

Ｑ．星の一筆書きはできるか？

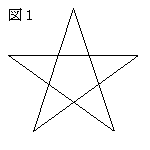
　この問いに対して、ほとんどの生徒は図１のような星を描いてくるであろう。

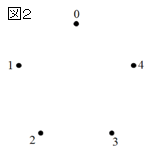
　この図は、図２のように正五角形の頂点に数字を振っておき、

　０ → ２ → ４ → １ → ３ → ０　の順に頂点を線で結ぶことで描くことができる。

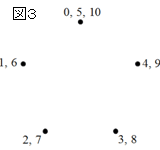
　また、図３のように数字を振ると（０と５と１０は同じ頂点を表す）、一筆書きは

　０ → ２ → ４ → ６ → ８ → １０　となり、０に２を５回足してできる数字の列で表せる。

　図３の頂点の数字は、頂点０から左回りに１，２，３，４…１０と振ったものである。この方が書き順の規則性はわかりやすい。その代わり、一つの頂点に複数の数字を割り当てることになる。図３の頂点においては、

　０＝５＝１０，　１＝６，　２＝７，　３＝８，　４＝９

　が成り立っている。これらイコールで結ばれている数は、５で割ったときの余りが一致している。

　つまり、図３における書き順０ → ２ → ４ → ６ → ８ → １０　に対して、それぞれの数を５で割った余りをとると、図２における書き順０ → ２ → ４ → １ → ３ → ０　になることがわかる。

　この考え方を利用して、今度は正８角形の頂点を結ぶ星の一筆書きを考える。
図４のように、正八角形の頂点に数字を振る。

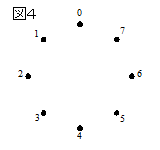
　正五角形のときと同様に、０に２を８回足して数字の列を作る。

　０ → ２ → ４ → ６ → ８ → １０ → １２ → １４ → １６ → １８

　それぞれ８で割ったときの余りをとると、

　０ → ２ → ４ → ６ → ０ → ２ → ４ → ６ → ０

　となる。これに従って頂点を線で結ぶと図５のようになり、一筆書きは失敗する。

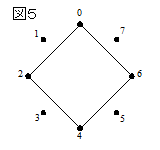
　そこで、今度は０に３を８回足して数字の列を作る。

　０ → ３ → ６ → ９ → １２ → １５ → １８ → ２１ → ２４

　それぞれ８で割ったときの余りをとると、

　０ → ３ → ６ → １ → ４ → ７ → ２ → ５ → ０

　となる。これに従って頂点を線で結ぶと図６のようになり、一筆書きができる。

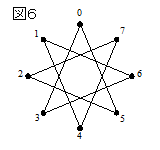
　失敗した図５の書き順は、途中で０が現れてしまっている。この一筆書きは、全ての頂点をちょうど１回ずつ通った後に０に戻るようにしたいので、最後の０に戻るまで０が現れてはいけない。従って、０にＮを８回足してできる数列

　０ → Ｎ → ２Ｎ → ３Ｎ → ４Ｎ → ５Ｎ → ６Ｎ → ７Ｎ → ８Ｎ

　について、Ｎ，２Ｎ，…７Ｎが８で割り切れないようなＮを選ぶ必要があるとわかる。
　これを満たすＮは、８と互いに素な数である。なので、例えば

　Ｎ＝１，　Ｎ＝３，　Ｎ＝５，　Ｎ＝７，　Ｎ＝９，　Ｎ＝１１，　Ｎ＝１３，　Ｎ＝１５，　…

　などは８と互いに素であるから、Ｎがこれらのとき一筆書きはうまくいく。

席替えへの応用

　ここで、先に例として挙げた３２人のクラスの席替えと同じ構造をもつ、正３３角形の頂点を結ぶ星の一筆書きを試みる。０にＮを３３回足してできる数字の列

　

　０ → Ｎ → ２Ｎ → ３Ｎ → ４Ｎ → ５Ｎ → … → ３１Ｎ → ３２Ｎ → ３３Ｎ

　において、Ｎ＝５２とすると（５２と３３は互いに素）、

　０ → ５２ → １０４ → １５６ → ２０８ → ２６０ → … → １６１２ → １６６４ → １７１６

　それぞれ３３で割ったときの余りをとると、

　０ → １９ → ５ → ２４ → １０ → ２９ → … → ２８ → １４ → ０

　となる。これに従って頂点を線で結ぶと図７のような星の一筆書きができる。

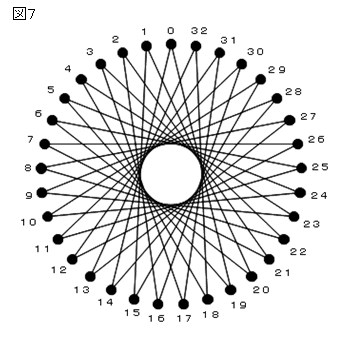
　最初の席替えの例では、５を選んだ生徒の新しい席は２９であった。そして、図７の一筆書きの第５画目の線分は２９番の頂点を結んでいる。この一筆書きは、席替えにおける余りがバラバラになっていることを視覚的に表しており、さらに、生徒が最初に選んだ数字がどのような規則で遷移しているかも表している。

席替えの規則性と生徒の思惑

　今回提示した「数学を用いた席替え」は、くじ引きのようにランダムな結果にはならず、はっきりとした規則性をもっている。ただ、生徒は数字を選んだ後に「かける数」がわかるため、作為的に自分の席を決めることはできないように思える。ところが、状況によっては、ある程度生徒の思惑通りにできてしまうこともある。

　例えば、２９人のクラスで席替えを行う場合、最後に割る数は３０になる。このとき、最初に１５を選んだ生徒は、後にかける数が何であっても、最後に求める余りは必ず１５になってしまう。また、５の倍数を選んだ生徒は最後に求める余りも５の倍数になる。これらは、割る数３０が５や１５を約数にもつために起こるものである。

　一般に、生徒が選んだ数Ａと最後に割る数Ｐに対して、ＡとＰの最大公約数をＤとすると、Ａを選んだ生徒はＤの倍数の席になる。

　なので、１５を選んだ生徒は、選んだ数１５と割る数３０の最大公約数が１５であるから、１５の倍数の席になる。そして、１～２９において１５の倍数は１５のみであるから、初めに１５を選んだ生徒は１５の席に決まる。

　もし、教室の席の配置が図８のような場合、一番後ろの席に行きたい人は初めに５，１０，１５，２０，２５のどれかを選んでおけばよい、ということになってしまうのである。

作為的な操作の回避

　前述のような決定的な規則性があるため、賢い生徒はその規則を見つけ出し、作為的に新しい席を選ぶこともできるであろう。この事態を回避するために、次のような方法を考える。

　２９人のクラスの席替えを例にとると、通常のやり方では、「１～２９の中から一つ選び、何倍かして３０で割った余りを求める」であったが、これを「１～３０の中から一つ選び、何倍かして３１で割った余りを求める」に変える。こうすると、最後に求める余りが３０になってしまう人が高確率で現れる。席番号は１～２９しかないので、この人の席は一旦保留にし、残りの２８人には新しい席に移動してもらう。すると、一か所席が空いているので、余りが３０の人はその空き席に行ってもらう。

　この方法では、割る数を３０から３１に変えることが目的である。割る数が３０だと、３０は多くの約数をもつため、作為的な操作をされやすい。ところが、割る数が３１だと、３１は素数であるから、席替えの決定的な規則性は無くなり、作為的な操作はできなくなる。

「数学を用いた席替え」に期待すること

　本稿で示した席替えは、単に席替えを楽に行うことが目的ではなく、この手法に隠れた数学的性質を生徒自らが疑問に感じ、探究することを望むものである。

　先で述べたように、この席替えは割る数の約数の個数分だけ決定的な規則が生まれる。決して難しい規則ではなく、席替えの仕組みに興味をもち、一生懸命考えた生徒であれば、何らかの事に気付けるはずである。そして、その生徒は次の席替えで自分に有利な選択ができるかもしれない。前項で「作為的な操作の回避」を示したが、これをただちに実行するのではなく、しばらく生徒の動向を見守るのも面白いだろう。

　「数学を用いた席替え」と「星の一筆書き」は数学的に同じ性質をもっており、これらは高校で学ぶ「合同式」や大学で学ぶ「巡回群」の例としても扱うことができる。最終的に教科書の内容と結びつけることで、生徒に高いレベルでの理解を促すことができるであろうと考えている。