Introduction

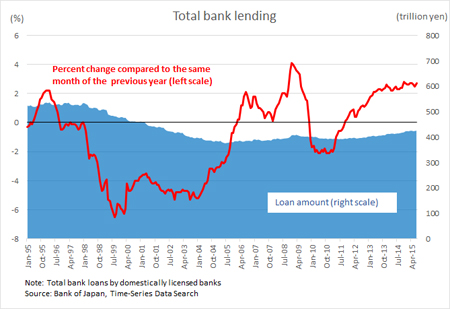
It is important to distinguish whether an economic event is driven by a supply factor or a demand factor in formulating an appropriate policy response. For instance, bank lending in Japan decreased substantially from the late 1990s to early 2000s (Figure). If such a decrease in bank loans derived from the reduction in bank loan supply due to banks’ massive non-performing loans in Japan at the time, then the priority for policy makers would be to resolve the bad loan problems on the part of lenders. On the other hand, if a decrease in bank loans derived from the reduction in loan demand by households and firms due to stagnant aggregate demand and deflation, then the appropriate policy response would be to stimulate the economy by macroeconomic policies.

However, it is often very difficult, if not impossible, to isolate loan supply shocks from loan demand shocks, because in most cases they may simultaneously affect each other. In the case of Japan’s declining bank lending, one of the root causes of bad loan problems was the collapse of the “bubble” in real estate and equity market in the late 1980s. The burst of the asset market bubble severely damaged the balance sheet of not only banks (lenders) but also firms and households (borrowers), resulting in the decline of loan supply and demand. Economists seem to have not yet reached an agreement on whether the primary cause of the decline in bank lending is on the supply side or demand side.

Recently, there has been significant progress in empirical literature on bank lending that successfully identifies loan supply shocks. In this essay, I will review two of those that make use of geographical borders and of the matched bank-firm loan-level data.

Difficulty of overcoming identification problems

The main challenge in identifying loan supply and demand shocks rests on the fact that economists cannot observe all relevant factors that affect supply and demand. As an example, consider the case where we estimate the following equation in order to examine the impact of banks’ non-performing loans (NPLs) on their loan supplies:

Change in bank loan=a+b×bank' s NPL+e　(1)

In this equation, a and b are estimated parameters (estimates) and e is the error-term. If banks with larger NPLs reduce loan supply more, then we expect that parameter b is a negative value.

Suppose that we obtain a negative estimate for b as expected using the Japanese banks’ data. Then, can we conclude that loan supply was reduced by the Japanese banks’ bad-loan problem, that is, by the supply side factor? Unfortunately, we cannot be so definitive in answering this question because loan demand factors are not considered in equation (1). In order to control loan demand factors, we need to estimate the following equation:

Change in bank loan=a'+b'×bank' s NPL+loan demand factors+e'　(2)

If equation (2) is correct, the estimate b in equation (1) is contaminated by loan demand factors. For instance, if banks with larger NPLs tend to have client firms whose loan demand were severely damaged by the collapse of the asset market bubble, then b in equation (1) is overestimated (b >b' ) because banks’ NPLs and their client firms’ loan demand were positively correlated.

In order to deal with this identification problem, extant empirical studies estimate the equation (2) that includes covariates representing loan demand factors. However, there is a limit to what extent economists can control loan demand. If there remain demand factors that are unobservable to economists, then the estimate b is still biased.

Solution 1: Use of geographical borders

One way to overcome the identification problem aforementioned is to focus on the loans to borrowers whose loan demand were unlikely to be affected by the collapse of asset market bubble in Japan. For instance, it is likely that the burst of the Japan’s bubble did not affect the loan demand of foreign households and firms. If that is the case, we should be able to identify the impact of supply shock by examining the loans of foreign borrowers that was made by Japanese banks with large NPLs.

For instance, in seminal works by Peek and Rosengren (1997, 2000), they examine whether the huge decline in stock prices and the surge in banks’ NPLs reduced Japanese banks’ ability to originate loans to U.S. borrowers and hence adversely affected their real activities.^[i] Apart from the bad loan problem, in a joint work with K. Hosono (Gakushuin University), D. Miyakawa (Hitotsubashi University), T. Uchino (Daito Bunka University), M. Hazama (Hitotsubashi University), H. Uchida (Kobe University), and I. Uesugi (Hitotsubashi University), I investigated whether the damage to banks inflicted by the Kobe Earthquake in 1995 negatively affected their client firms’ investment.^[ii] It is conceivable that the massive earthquake had serious damages on both lenders and borrowers located inside the earthquake-affected areas, but did not have direct impacts on firms located outside the affected area. In this study, we have isolated the loan supply shock by focusing on the firms located outside the area and comparing those that transacted with the damaged banks and with the undamaged banks.

Solution 2: Use of bank-firm matched loan-level data

The studies cited above are useful in identifying loan supply shocks, but they have a caveat in that we cannot make inferences on bank loan supply shocks at the “epicenter” of the financial crisis and the natural disaster.

Some recent studies overcome this difficulty by making use of the data on firms’ borrowings from multiple banks. The basic idea is as follows. Suppose firm i located in Japan obtains loans from two banks, say bank 1 and bank 2. If we know the amount of individual loans from these two banks, the equation (2) can be rewritten as follows.

Change in loan by bank 1 to firm i=a'+b'×bank 1' s NPL+loan demand factors+e' (i,1)
Change in loan by bank 2 to firm i=a'+b'×bank 2' s NPL+loan demand factors+e' (i,2)

By differencing two equations above, we obtain

(Change in loan by bank 1 to firm i )-(Change in loan by bank 2 to firm i )
=b'×(bank 1'sNPL-bank 2'sNPL)+{e' (i,1)-e' (i,2)}　(3)

And we can see that loan demand factors vanish by taking differences. In other words, since loan demand is a common factor across loans from bank 1 and bank 2, the relative difference between loans from bank 1 and bank 2 can be attributed to the supply side factor, which is the banks’ NPLs in this case. By estimating equation (3), we can examine the impact of banks’ bad loan problems on domestic loans.

Earlier studies on bank lending mostly used time series aggregate data or bank-level data. As the bank-firm matched loan-level data became more available, economists started to employ the above identification strategy. Regarding Japan’s bad loan problems, there are studies that examine the impact of declining real estate prices in the early 1990s (Gan 2007) and the impacts of public capital injections to major Japanese banks in 1998 and 1999 (Giannetti and Simonov 2013) on their domestic loan supply using bank-firm matched loan data.^[iii] In a similar vein, in an ongoing joint research project with K. Aoki (University of Tokyo) and others, I am investigating the impact of lowering long-term interest rate in the 2000s on bank loan supply, which is driven in part by monetary easing by the Bank of Japan, using bank-firm matched loan data.

Closing remarks

The identification strategies reviewed above can be applied to many fields of economic and social phenomena. I hope that our understanding of economic activities deepens with the increased availability of detailed dataset.