Here I will explain the first half of the joint research by myself and Dr. Toyabe of my research laboratory, and Dr. Sagawa, Professor Ueda and Professor Sano of the University of Tokyo's School of Science, which was published in Toyabe, Sagawa, Ueda, Muneyuki, and Sano, Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality, Nature Phys. 6, 988-992(2010). Starting with the second law of thermodynamics and Maxwell's demon, I will try to explain it in relatively simple terms.

1. The second law of thermodynamics

The second law of thermodynamics is an extremely rare physics law which uses no stated formula and is often expressed in two ways.

Clausius theorem

No process is possible whose sole result is the transfer of heat from a body of lower temperature to a body of higher temperature.

Kelvin theorem

No process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work.

By violating the Clausius theorem, a difference in temperature can be made from a place with no temperature difference, and by using that to expand an object, the Kelvin theorem can be violated. If the Kelvin theorem is violated, the work obtained will create frictional heat and raise the temperature, in turn going against the Clausius theorem, meaning both are saying essentially the same thing. This second law of thermodynamics is one of the most fundamental laws of nature which cannot be broken.

2. Maxwell's demon

The second law of thermodynamics mentioned above is an unbreakable law but many people have provided ideas to try and violate that law from long ago. One of the most famous of those attempts is Maxwell's demon, devised by James Maxwell (1831-1879), where he tried to violate the Clausius theorem and create a temperature difference. Here, high temperatures indicate that the molecules which make up a substance are moving in an irregular, vigorous state, whereas low temperatures indicate the molecules are moving slowly.

It is a fact that all matter fluctuates in accordance with temperature, and those fluctuations are called thermal fluctuation. For example, when water molecules below the surface collide 10¹³ times per second, they are moving at an average speed of several 100 meters per second. Micrometer-sized particles which are stimulated by these water molecule collisions constantly display an irregular movement called Brownian motion. This Brownian motion is also a type of thermal fluctuations.

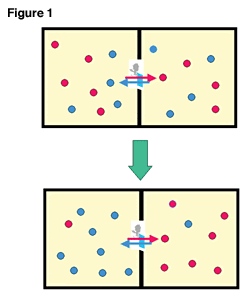
Therefore, to create a temperature difference where the right side of a gas-filled container is hot and the left side cool, gas molecules moving faster than the average speed must be gathered on the right with slower than average gas molecules gathered on the left.

Here, Maxwell thought of a container divided into left and right parts with a door that could be opened and closed by a hypothetical demon (Figure 1). When the slower molecules in the right chamber approach the door, the demon will quickly open and close the door and let them pass to the left chamber, and when the faster molecules from the left chamber approach the door, the demon would once again open and close the door quickly to let them pass through to the right side. By repeating this, the faster gas molecules will gather on the right and the slower particles to the left, thus creating a temperature difference between the left and right chambers.

Because the gas molecules do not come into contact with anything while passing through the door, they receive no energy. In other words, because of the presence of Maxwell's demon, the gas molecules within the container receive no energy, and furthermore, allows a difference in temperature. This can be seen to be a violation of the aforementioned Clausius theorem. Because of that, there has been great controversy surrounding Maxwell's demon since its appearance in 1867. But there has to be a trick somewhere.

Here, I will summarize what Maxwell's demon does.

1. Observes the speed of gas particles.
2. Memorizes the information gained from the observations.
3. Operates the door to let gas molecules pass through.
4. Deletes the previously memorized information and prepares for the arrival of the next molecules.

As explained before, through the process of operating the door, the energy levels of the molecules remain unchanged. In doing so, energy needs to be used somewhere in steps 1, 2, or 4 of the demon's operation to prevent a violation of the second law of thermodynamics. But there is essentially information involved when talking of these steps, information which wasn't available in physics of the day.

A temporary solution to this problem was discovered in 1961 in the form of Landauer's Principle. Landauer showed that energy is required in step 4, where information is deleted. Furthermore, one of the main figures of our research, Dr. Sagawa, along with Professor Ueda, showed that there is a set limit of required energy in combined exchanges of information acquisition and deletion. Through this research, it was revealed that Maxwell's demon was secretly using energy. Accordingly, the realization of Maxwell's demon, in current understanding, becomes using energy to acquire information, not to directly move the gas molecules, but to control that movement.

3. Realization of Maxwell's demon

I hope that you understand that what I have explained so far shows that Maxwell's demon is not in complete violation of thermodynamics. But it is not so simple to make Maxwell's demon.

First of all, Maxwell's demon moves the gas molecules without coming in direct contact with them, but that is because the molecules are traveling around at various speeds and directions spontaneously, and when the particles approach, he must open and shut the door quickly.

By the way, it is actually normal for micrometer-sized matter to fluctuate, without doing anything at various velocities by thermal fluctuation. These days, the world of nanotechnology actually deals with extremely minute substances, so it tries to suppress thermal fluctuation by lowering temperatures and using mass energy, meaning there are such places in the world in which Maxwell's demon can be involved. Because of these places, the realization of Maxwell's demon is interesting not only in physics, but it also has a place as a challenging aim in the technical aspect of high speed and precise control in the microscopic world. If this can be achieved, it can be used in place of thermal fluctuation control, and become an epoch-making method for regulating matter movement, go against the way of thinking up until now. It was Dr. Toyabe, the main figure in this research, who accepted the challenge of this experimental side.

Here we cannot construct a real experimental system in the form just imagined by Maxwell, so we aimed to build something similar that would move particles from a low energy position to a high energy position, or in physics terms, give the particles potential energy.

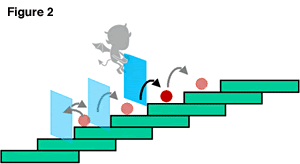
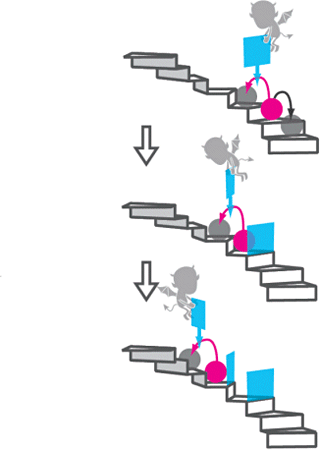
First of all, the information Maxwell's demon used was the velocity of the gas molecules, but we decided to use the position of the molecules. Then, the demon controlled the traffic of gas molecules which came near through the door. In our case, we placed a divider behind particles which had happened to rise to a position of high potential (think of particles which have reached the top of a flight of stairs) to stop them from going back (Figure 2). In the microscopic world, particles occasionally rise to places of high potential due to vigorous thermal fluctuation. Maxwell's demon was in one placed and divided many molecules to create fluctuating temperatures, but we inserted a divider while following one particle, and chased it to a high position. Because the divider is only placed behind the particle there is no direct influence on the particle, so in the same way as Maxwell's demon, information regarding the particle is acquired and the potential energy of that particle is raised without directly giving energy to it.

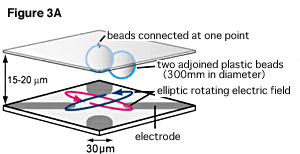
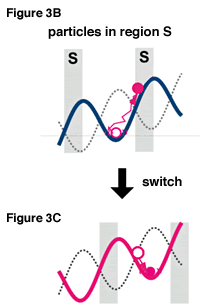
For this, our laboratory's F1-ATPase rotating electric field equipment, used for rotating molecular motor research, was helpful. This equipment has four minute electrodes deposited on the surface of a sheet of glass, and can create various electric fields by adding voltage to the electrodes. In F1-ATPase research, potential by the electric field is applied to two adjoined 0.3 micrometer diameter plastic beads which are connected to the F1-ATPase. With this equipment, we connected the beads directly to a single point on the glass surface without using F1-ATPase (Figure 3A), and controlled the voltage applied to the electrodes, creating a potential spiral staircase like the one shown in figure 3B. On top of this kind of potential, the plastic beads move in a rotating Brownian motion, occasionally starting to rise to the top of the peak to the right of the diagram, and sometimes going over the peak, but usually move in the lower left side. When the plastic beads are observed by microscope, when their position happens to come part way up the slope of potential on the right (gray area S on figure 3B), the voltage is changed, and hence the potential is changed as represented by the dotted line on figure 3B (also equal to the red line on figure 3C). It may seem simple, but we have overcome several extremely difficult tasks such as creating accurate potential, detecting the position of the beads instantaneously and quick changing the potential profile. By changing the potential in this way (Figure 3C), the beads are placed on the right downward slope by the new potential, making it difficult to go to the left. This corresponds to the insertion of the divider. Then we can expect the beads to follow the downward slope into the right valley. The bottom of this valley is higher than the valley of the original potential valley, meaning the beads have risen to a slightly higher position. By repeating this process, the beads gradually climb the potential slope to the right of the diagram. Here, we must pay attention to that the energy was supplied solely by thermal fluctuation when the beads move up the slope. In other words, the information measured of the beads being in area S is converted to a starting potential energy without directly applying energy. This is the Maxwell's demon of this experiment.

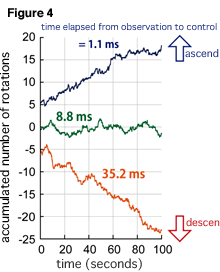
By the way, it is stated that to realize Maxwell's demon, quick operation is necessary. Actually, even if the beads are in area S when observed, if we don't work quickly, they may be outside of area S when the potential conversion is made. Here, as shown in figure 4, we observed the movement of the beads by changing the time taken from measuring the position to changing the potential. It is certain that the beads rise up the slope when the conversion is made in 1.1 milliseconds and remain virtually unchanged after 8.8 milliseconds, but after 35.2 milliseconds, even after changing the potential, the beads end up going down the slope.

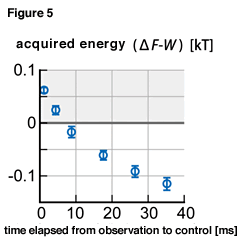
If the beads are outside area S when the potential is changed, there are times the beads receive energy from the electric field which creates the potential. Conversely, when the beads are in area S at the time of potential conversion, they give energy to the electric field. The exchange of energy between the beads and electric field is strictly calculated and compared with the energy acquired by the beads rising up the slope in figure 5. When the potential is changed quickly, the amount of energy acquired by the beads exceeds the energy received from the electric field. Our experiment is the first in where the amount of energy gained by a substance exceeds that of the energy added from outside has been accurately shown. This difference in energy comes from thermal fluctuation, and at first glance, appears to violate the Kelvin theorem, but this is possible because energy was used to acquire the information of the beads position. If the energy required to measure the position is included in considerations, the second law of thermodynamics has not been violated.

The original manuscript continues with important content such as the relationship between the amount of information acquired from the measurements and the energy acquired by the beads, and verification of the generalized Jarzynski equality, but unfortunately there isn't enough space to write about this. In order to understand these, there are many things that should be studied from the basics, so I suggest to those of you who want to learn, to try studying from the basics, because the eye-opening world lies in the future.