Introduction

There have been rapid improvements in measurement technology and computer performance in recent years. As a result of these improvements, new types of data have been measured and stored, and statistical analysis technology has been developed which makes full use of computers. In coming times, decisions based on such data will be required in a variety of areas, from advanced scientific technology to everyday life. Therefore, it can be said that the importance of statistical science has increased even further.

My field of research is statistical science, and the objective of my research is to develop new statistical methods for a variety of different types of data. However, in this article, I will emphasize the perspective of practical application and introduce examples of functional data analysis and multiple testing methods from the research themes of my laboratory. Also, I will introduce statistics in sports which is being advanced through joint research with a corporation.

Functional Data Analysis

As I stated previously, recent advancements in measurement technology have made it possible to acquire various formats of data. Functional data is one type of data format. Individual data is observed in the format of a linear function; in other words, a curved line (or curved surface). functional data analysis is a statistical method for handling such functional data.

This graph is an example of the average speed pattern of vehicles driving on a certain freeway. The horizontal axis shows the time of day (0:00 to 24:00) and the vertical axis shows speed. Vehicles on the blue freeway maintain almost the same speed throughout the entire 24-hour period. However, it can be seen that the red and green freeways are subject to a rush hour period, or a period when vehicle speed is reduced. This data is measured every 5 minutes and therefore is obtained through discrete points. However, in essence, these can be thought of as measurement of a curved line.

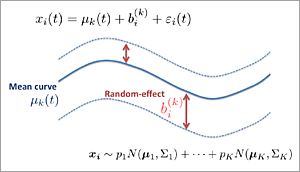
When a large number of such functional data is being obtained, classification is performed for each similar freeway of the change patterns. We are now trying to develop a new method, which consists of a combination of complicated models including a mixed effect model, a GMM model, and a nonparametric Bayes model, to search for the appropriate number of groups.

By using these various statistical models, it may be possible to reveal structures which reside deep within data and which cannot be seen by simply looking at complicated data.

Multiple Testing Methods

Multiple assay is a method for the simultaneous verification of multiple hypotheses.

For example, in the field of genome analysis, multiple assay and a variety of other statistical methods are used in order to approach problems such as gene network estimation which uses gene expression data (diagram) to search the control relationships between genes, as well as identification of disease-associated genes through the use of single-nucleotide polymorphism (SNP).

Generally speaking, such fields contain an extremely large number of hypotheses which must be verified simultaneously. These hypotheses possess mutual unknown relationships and also possess sparse (only an extremely small number of observation values have an effect) structures in some cases. Such characteristics render classical statistical methods ineffective.

In such cases, it is possible to apply a permutation method and a bootstrap method, both of which are statistical analysis that use computers. However, theoretical certification been denied for methods which are normally used in the current field of genome analysis. Indeed, several theses which point out theoretical problems have been published in recent years. Currently, we are working to verify the theoretical validity of such multiple testing methods and to develop new multiple testing methods. The development of statistical methods such as multiple testing methods will become a catalyst for opening new worlds in genome analysis, a field with many unknown areas.

Statistics in Sports

Statistical analysis is also utilized in the world of sports. Statistical analysis is essential for conducting objective evaluation in a variety of areas such as the selection of appropriate strategy, the assessment of athletes and the management of lineups. I would like to introduce such the use of statistics by focusing on baseball, one of the most advanced sports from the perspective of statistical analysis.

Since about 1980, a baseball statistical analysis method known as SABRmetrics (a term formed by combining SABR, abbreviation of the Society for American Baseball Research, and metrics, a term representing measurement) has seen widespread use in the United States. Some people may have heard of SABRmetrics from Billy Beane, an MLB general manager who is known for transforming poor franchises into contending teams.

Instead of relying on traditional values, SABRmetrics is based concept of using data to conduct objective evaluation of strategy and athletes. For example, statistics such as batting average, RBI and number of home runs are used to evaluate batters in Japan. However, it is not possible to appropriately measure an athlete's contributions to team victories when using such numbers. For example, even though a BB (base-on-balls) and a single hit produce exactly the same result, BB statistics are not evaluated. Another example is that it is not possible to earn RBI if no runners are on base. Instead of using such conventional statistics, SABRmetrics evaluates athletes through unique indeces such as OPS (on-base percentage + percentage of extra-base hits). This index has a high correlation with runs scored, while runs scored and runs yielded have a high correlation with wins and losses. Therefore, it can be said that the use of indeces such as OPS make it possible to an athlete's contribution to victory. Similarly, SABRmetrics proposes a large number of other indeces which objective evaluate positions such as pitchers and catchers, as well as the fielding and batting of fielders.

A current trend in the United States is to convert into data the trajectory of thrown balls and the trajectory of movement by athletes when fielding. This data is analyzed and applied through high-level statistical analysis. Unfortunately, it is no exaggeration to say that conditions in Japan are several dozen years behind the technology used in the United States. A classic example of this gap is the sacrifice bunt. It has been statistically proven that sacrifice bunts actually decrease the expectations for scoring runs during that inning (as well of decreasing the probability of scoring). For this reason, almost no sacrifice bunts are used in the Major League Baseball. However, the concept of sacrifice bunts matches the spirit of self-sacrifice which is inherent among the Japanese, and sacrifice bunts are therefore used as a fundamental tactic in Japan. Some people may think that conditions are different in Japanese baseball, which is often referred to as small ball. Unfortunately, it has also been confirmed that the use of sacrifice bunts lowers the expectations for runs (probability of scoring) in Japanese baseball. (Personally, I have reached the same conclusion when performing analysis using a statistical method known as the propensity score method.)

We are currently researching a correct evaluation method for starting pitchers. In Japanese professional baseball, pitchers are normally evaluated using statistics such as ERA, wins and losses. However, these statistics are not appropriate for evaluating pitchers. For example, even if a starting pitcher throws well, he cannot earn a victory if batters do not support him by scoring runs. Furthermore, the starting pitcher will lose his right as the winning pitcher if runs are yielded by relief pitchers. Conversely, there are cases in which a pitcher who yields a great number of runs can receive a victory through the support of his team's batters. Therefore, we consider the use of a Support Neutral Win (Loss) method. This method determines the number of wins (or losses) that a starting pitcher would have if his team's batters and relief pitchers performed on a standardized level. In other words, this index can appropriately evaluate starting pitchers by removing all factors other than the pitcher himself. We are currently working to create a Japanese method of this index.

Until known, I have limited the scope of discussion to baseball. However, in the future, I would also like to apply statistical analysis to soccer. I am sure that most people still have fresh memories of Japan's performance in the 2010 FIFA World Cup. In this most recent World Cup, the total distance run by each athlete in one game was calculated. In Japan, it was widely reported that players such as Endo and Honda run 11 kilometers in a single game. The distance run was calculated from trajectory data acquired by following the movement of players and balls by camera. However, this trajectory data has many other applications other than simply calculating distance run. We would like to use this valuable yet under-utilized data in order to further promote the sport of soccer. Furthermore, by developing new statistical models, we would also like to conduct research with the goal of furthering statistical science.

Conclusion

In this article, I introduced the research themes of our laboratory, as well as the accompanying practical applications. Statistical science is utilized in a variety of fields as a method for uncovering new knowledge. In order to respond to such needs, researchers in statistical science are working everyday to develop new theories and methods.

Decision-making through statistical evaluation is not limited to the advanced scientific technology or specialized fields described above. Actually, such judgments are given priority within our daily lives. For example, a variety of graphs are used by media such as television and newspapers. However, the statistics or the graphs are often incorrect (or perhaps intentionally misrepresented?). In order to lead a social life as an intelligent citizen who is capable of correctly interpreting information, it is important to acquire statistical literature. This importance is expressed in the new educational curriculum guidelines of elementary schools, junior high schools and high schools. These new curriculums for mathematics and science place emphasis on statistics and probabilities. Our entire academic society is working to spread statistics through a variety of events and campaigns, as well as by providing a great number of educational materials such as digital materials developed by our group (created in 2009 through the support of the Japan Science and Technology Agency). I hope that this article will create interest in statistical science among readers.