Research in Algebraic Geometry
Kiwamu Watanabe/Associate Professor, Faculty of Science and Engineering, Chuo University
Area of Specialization: Algebraic Geometry
1. The Nobel Prize and the Fields Medal
One of the most prestigious awards in science is the "Nobel Prize". There is no need to explain this award in detail here, but you might know that mathematics is not included in its fields. One theory is that this exclusion was due to a poor relationship between a certain mathematician and Alfred Nobel. On the other hand, there is the "Fields Medal", often called the "Nobel Prize of Mathematics". The Fields Medal is awarded every four years at the International Congress of Mathematicians (ICM) to outstanding mathematicians under 40 (between two and four recipients). Japanese recipients of the Fields Medal include Professors Kunihiko Kodaira, Heisuke Hironaka, and Shigefumi Mori. All three of these mathematicians specialize in "algebraic geometry", indicating that algebraic geometry has been a thriving area of mathematical research in Japan.
2. Linear Algebra and Algebraic Geometry
What is algebraic geometry? Generally, the study of numbers, equations, and operations is called algebra, while the study of shapes and spaces is called geometry. Algebraic geometry starts with considering the solution sets of algebraic equations geometrically. For instance, consider the following system of linear equations:
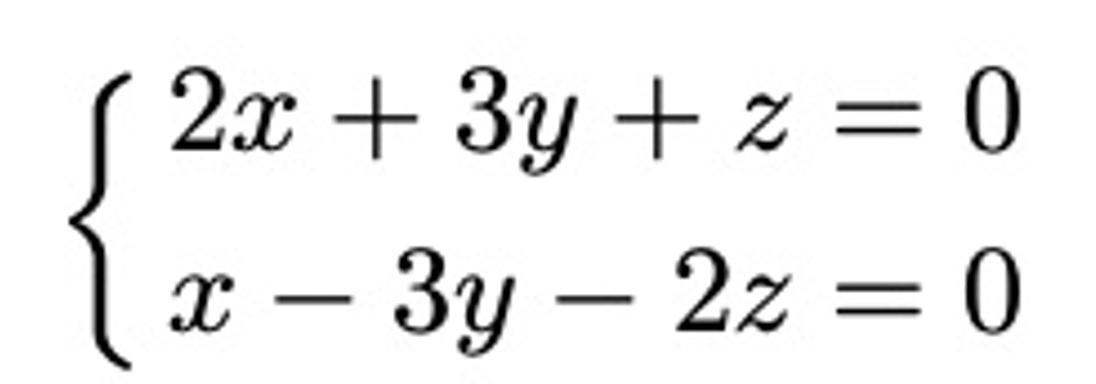
Even without knowledge of university-level mathematics, solving this system of equations is straightforward. More complex systems of linear equations can also be solved algebraically using "elementary row operations", a method typically taught in first-year university linear algebra courses. Geometrically, this system of linear equations can be interpreted as the intersection of two planes in xyz-space:
![]()
In algebraic geometry, the solution sets of algebraic equations are regarded as geometric objects (such as curves or surfaces), and their properties are studied.
Thus, an equation can be viewed algebraically or geometrically, depending on the perspective. Learning the theory of systems of linear equations (linear algebra) usually takes about a year. Even within linear algebra, abstract theories like vector spaces can be very challenging for beginners. Considering more complex systems such as quadratic, cubic, quartic, 100th-degree, or 1000th-degree equations, the situation becomes increasingly complicated, making their analysis difficult. Algebraic geometry deals with systems of equations of general degrees.
3. Algebraic Varieties
Let's explain the shapes dealt with in algebraic geometry more precisely. Using as few mathematical symbols as possible might be somewhat inaccurate, but please bear with me. In high school, the figure represented by y = x in the xy-plane was a straight line, which can also be written as y − x = 0.
Such figures expressed as (some) polynomial = 0 are called algebraic varieties. Strictly speaking, an algebraic variety is a figure that can be glued together from such figures, but for simplicity, we'll refer to the solution sets of some algebraic equations as algebraic varieties. You may feel it's complicated, but in high school, you dealt with various examples of algebraic varieties. For instance, besides straight lines, unit circles, parabolas, hyperbolas, and ellipses are all algebraic varieties. When drawn in the xy-plane, these figures all have smooth outlines without sharp or intersecting points. Such algebraic varieties that are smooth at every point are called non-singular algebraic varieties. For simplicity, "variety" here refers to non-singular algebraic varieties.
4. My Research
In high school mathematics, you learned how to sketch the shape of the graph y = f (x) using the first and second derivatives of the function f (x). By using the first derivative, you examined the increase and slope of the function, and by using the second derivative, you determined the concavity and extrema of the function. For each point P on a variety X, a small region around it resembles Euclidean space, allowing the definition of a tangent space at that point. The tangent space collects tangent vectors at point P and provides a local linear approximation of the variety. Collecting all the tangent spaces of a variety gives the tangent bundle, corresponding to the first derivative obtained when sketching the graph. Additionally, there is the concept of curvature in differential geometry, which measures the shape of the variety. Curvature corresponds to the second derivative obtained when sketching the graph (more accurately, the curvature of the graph y = f (x) can be described using the second derivative and the first derivative).
For the past few years, I have been studying the structure of varieties from the perspective of the positivity of tangent bundles. The positivity of the tangent bundle can be thought of as representing the curvature of the variety. This line of research started with Professor Shigefumi Mori's resolution of the Hartshorne conjecture, which states, "Non-singular projective varieties with ample tangent bundles are limited to projective spaces". This conjecture claims that the most basic shapes with positive curvature (non-singular projective varieties) everywhere are projective spaces. This result was also the starting point for the subsequent minimal model theory and significantly impacted the history of algebraic geometry. I have been studying the structure of varieties with nef tangent bundles and varieties where the exterior power of the tangent bundle is nef as a generalization of the Hartshorne conjecture. The condition "ample" corresponds to a value greater than zero, while "nef" corresponds to a value greater than or equal to zero. Although the difference is whether zero is allowed, this condition creates a significant distinction. Indeed, while varieties with ample tangent bundles are limited to projective spaces, there are countless varieties with nef tangent bundles, including symmetric figures called homogeneous varieties. I am researching the Campana-Peternell conjecture (CP conjecture) on varieties with nef tangent bundles[2], the structure of varieties with more general nef tangent bundles[1], the structure of varieties where the exterior power of the tangent bundle is nef[3]・[4], and more generally, Fano varieties. For a series of achievements related to the CP conjecture, I was awarded the Takebe Prize by the Mathematical Society of Japan in 2018.
5. Outreach Activities and YouTube
One of the challenges in algebraic geometry is explaining the research content. Even students who have completed a master's degree often cannot fully understand what their supervisors are researching. On the other hand, the importance of outreach activities is increasing yearly. I upload videos related to my research and undergraduate-level lectures on my YouTube channel (www.youtube.com/@Qmath). The first half of this article is based on the content of the video "What is Algebraic Geometry?" Various videos, including those for non-experts, preparatory videos for lectures at Chuo University, and videos related to intensive lectures at the University of Tokyo and Nagoya University, are available. If you are interested, please take a look.
References
[1] Akihiro Kanemitsu, Kiwamu Watanabe, Projective varieties with nef tangent bundle in positive characteristic, Compos. Math. 159 (2023), no. 9, 1974 ‒ 1999.
[2] Roberto Mun˜oz, Gianluca Occhetta, Luis E. Sol´a Conde, Kiwamu Watanabe, and Jaroslaw A. Wi´sniewski, A survey on the Campana-Peternell conjecture, Rend. Istit. Mat. Univ. Trieste, 47:127 ‒ 185, 2015.
[3] Kiwamu Watanabe, Positivity of the second exterior power of the tangent bundles, Adv. Math. 385 (2021), Paper No. 107757, 27 pp.
[4] Kiwamu Watanabe, Positivity of the exterior power of the tangent bundles, Proc. Japan Acad. Ser. A Math. Sci. 99 (2023), no. 10, 77 ‒ 80.
Kiwamu Watanabe/Associate Professor, Faculty of Science and Engineering, Chuo University
Area of Specialization: Algebraic GeometryKiwamu Watanabe was born in Yokohama City in 1984. In 2006, he graduated from the Department of Mathematical Sciences, Waseda University. In 2008, he completed the Master’s Program in the Department of Mathematical Sciences, Waseda University. In 2010, he completed the Doctoral Program in the Department of Pure and Applied Mathematics of the Graduate School of Fundamental Science and Engineering, Waseda University. He holds a Ph.D. in science. He served as a Research Fellow for Young Scientists of the Japan Society for the Promotion of Science (JSPS) (DCI and PD; Waseda University), a Research Fellow for Young Scientists of JSPS (PD; the University of Tokyo), and Assistant Professor in the Graduate School of Science and Engineering, Saitama University before assuming his current position in 2020.
He currently researches the structure of algebraic manifold from a perspective of positivity of tangent bundle and the structure of Fano manifolds. He is making ardent efforts in outreach activities by releasing videos related to his lectures on YouTube and engaging in social media activities.









