How will we use data and information?

Not a day goes by without seeing the words "AI" and "data science." Under these circumstances, it goes without saying that modern society generates an enormous amount of data. In addition to the digitization of various systems, most people constantly carry a device connected to the Internet and record their lives on the Internet without being asked to do so. As a result, we are steadily accumulating data that records every movement in society. Of course, even though such data is being accumulated, there are still many issues; for example, the data is not stored in an easy-to-use format, or not made public in a format that can be used by anyone. Even so, it is a fact that the trend of digitization is progressing steadily throughout our world.

However, even if there is an enormous amount of data, the mere existence of data is useless. Value can only be created by extracting useful information from data and then using that information. Among these two aspects, the technology for extracting information from data has made remarkable progress in recent years. By using machine learning, it is becoming possible to classify large amounts of data more accurately by AI than by humans, and research is also progressing on technology for discovering hidden trends in data. This poses the question, "what about the technology for using the information extracted in this way?"

Decision-making is the process of making decisions about system operation, design, and measures based on the acquired information. My recent awareness of the problem is that the evolution of decision-making methods has not caught up with the speed of developing methods of acquiring information. In this article, I would like to briefly introduce a method called adaptive optimization, which I have been working on for the past few years based on my awareness of this problem.

Mathematical optimization in decision-making technology

I would like to touch on mathematical optimization before discussing adaptive optimization. Mathematical optimization is a technique for using a computer to solve a computational problem that seeks the best option from among various options. When making a decision using mathematical optimization, we describe a mathematical optimization problem that expresses the conditions that must be satisfied and the quantities that we want to optimize. Based on these conditions, calculating the solution of this mathematical optimization problem provides us with plans and measures to be implemented in the future.

Mathematical optimization research has a long history. It is an important foundation which underpins the information technology of today. For example, one of the killer applications of mathematical optimization is route finding, which searches for a route from one point to another. Although this seems like a commonplace technology nowadays, it is no easy task to select the best route from thousands, tens of thousands, or hundreds of millions of routes. This is where mathematical optimization shows its worth.

Mathematical optimization is an important tool for decision-making, but it can seem insufficient when trying to utilize diverse information. For example, instead of returning a single definitive prediction, many machine learning algorithms will output the probability distribution of the prediction result. In other words, the results will be something like "it will take 20 minutes with probability 80% and 30 minutes with probability 20% via this route." In fact, Google Maps, which is likely used by many readers of this article, returns three types of predictions (pessimistic, normal, and optimistic) when asked for the travel time between two points via the API. It is difficult to utilize this kind of information in the conventional framework of mathematical optimization.

Adaptive optimization: Optimization under uncertain conditions

Adaptive optimization is one approach to decision-making under conditions in which uncertain information is provided (like the situation introduced above). Adaptive optimization is a framework that expands the framework of ordinary mathematical optimization. It seeks to achieve a level of performance superior to ordinary mathematical optimization methods by devising a plan from information with elements of uncertainty or ambiguity, executing a portion of the plan, and then updating the plan based on information acquired in the process of execution.

Here, I'd like to introduce a concrete example in order to give my readers a feel for the power of adaptive optimization. In the road network shown in Figure 1, which is the shortest route from the origin to the destination? In this network, there are two types of routes from the origin to the destination: a route through point A and a route through point B. However, there are many parallel roads from point B to the destination. The number written on the side of the road is the time required when taking that road. However, it is assumed that the time required for each road from point B to the destination is determined probabilistically. The time required is 2 with probability 0.99, and is 0 with probability 0.01. The time required for each road is decided independently.

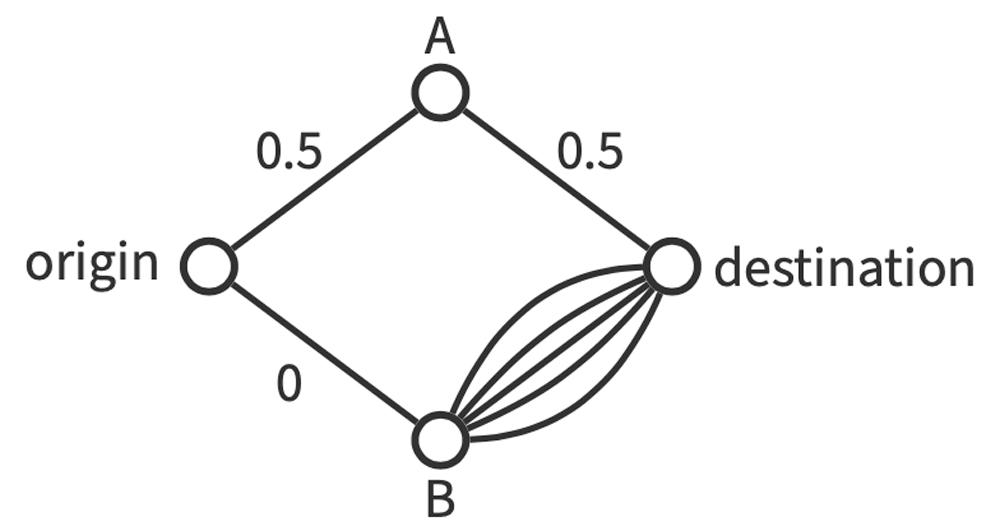
Figure 1: Example of road network

In an optimization problem defined probabilistically in this way, the usual approach is to define the solution with the best expected value for the evaluation scale as the optimal solution. In the example above, the time required for the route through point A is always 1, and the expected value of the time required for the route through point B is 1.98 regardless of which of the parallel roads is taken. Here, it is clear that the expected value of the time required is minimized by taking the route through point A.

However, do you realize there is a better way? That is, after going from the destination to point B, and after observing the time required for each road from point B to the destination, you should then choose the fastest road and head to the destination. The probability that one road connecting point B to the destination will have a travel time of 0 is very small. However, if there are many parallel roads, there is a high probability that at least one of them will have a travel time of 0. Therefore, if such a strategy is allowed, the expected value of the time required from the origin to the destination is almost 0 (the exact expected value depends on the number of roads between point B and the destination).

Of course, some people may say that such a strategy in unfair. This all depends on whether you are allowed to make such observations during your optimization. Adaptive optimization aims to realize more efficient optimization by utilizing such features under the condition that probabilistic events can be observed at the execution stage of the algorithm.

Conclusion

In this way, adaptive optimization has more potential than conventional mathematical optimization. Of course, there are numerous problems. As you can imagine, problems to which adaptive optimization is applied are structurally more complex and difficult than those to which conventional mathematical optimization is applied. In many cases, it is not yet known whether such problems can be solved efficiently. My current research theme is to deepen understanding so that this technology can be used.

Takuro Fukunaga／Professor, Faculty of Science and Engineering, Chuo University
Area of Specialization: Mathematical Informatics

Takuro Fukunaga was born in Nagoya City in 1981. He graduated from the Faculty of Engineering, Kyoto University in 2003. He completed the Master’s Program in the Graduate School of Informatics, Kyoto University in 2005. He completed the Doctoral Program of the same graduate school in 2007. He holds a Ph.D. in informatics.
He served as Assistant Professor in the Graduate School of Informatics, Kyoto University, Project Associate Professor at the National Institute of Informatics, researcher at the RIKEN Center for Advanced Intelligence Project, and Associate Professor in the Faculty of Science and Engineering, Chuo University before assuming his current position in 2021.

He is engaged in research on information engineering, especially theories of discrete algorithms and their application to decision-making.

• Share articles
• 
• 
•